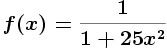
MATLAB sopii hyvin erilaisten numeeristen ongelmien ratkaisuun. Alla muutamia perusongelmia ja niihin liittyviä MATLAB-esimerkkejä.
Lineaarinen yhtälöryhmä ratkeaa MATLABin takakeno-operaatiolla. Jos yhtälöitä on enemmän kuin tuntemattomia (kerroinmatriisin aste on pienempi kuin tuntemattomien lukumäärä) saadaan pienimmän neliösumman ratkaisu.
Yhtälöryhmä
| 10x1-7x2 | = 7 |
| -3x1+2x2+6x3 | = 4 |
| 5x1-x2+5x3 | = 6 |
» A=[10,-7,0;-3,2,6;5,-1,5]
A =
10 -7 0
-3 2 6
5 -1 5
» b=[7,4,6]'
b =
7
4
6
Yhtälöryhmä ratkeaa takakenolla
» x=A\b
x =
0
-1
1
ja ratkaisun voi tarkistaa matriisikertolaskulla:
» A*x
ans =
7
4
6
Tarkastellaan vektoreihin x ja y talletettuja
datapisteitä. Polynomi-interpolaatio datapisteille saadaan
polyfit-funktiolla. Se palauttaa sovituspolynomin
kertoimet, joita vastaavan polynomin arvoja voi laskea
polyval:n avulla.
Interpoloituja taulukkohakuja voi tehdä interp1-
ja interp2-funktioilla.
Esimerkki: Valitaan Rungen funktiosta
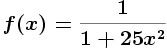
x=linspace(-1,1); plot(x,rungefun(x),'k'); hold on; axis([-1,1,-0.4,1.3]) for n = [4,6,8,10,20] xp = linspace(-1,1,n); yp = rungefun(xp); plot(x,polyval(polyfit(xp,yp,n-1),x)); end hold off; axis normal;
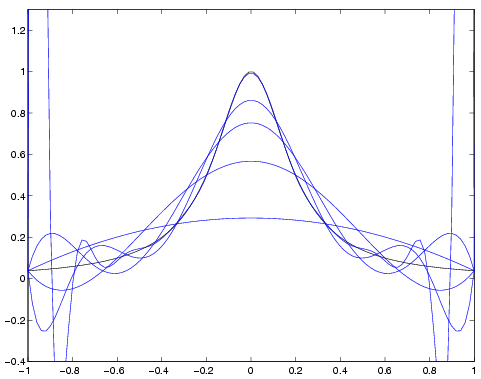
Datan sovitus annettuun funktioluokkaan (malliin) on sukua interpoloinnille. Polynomin voi sovittaa, joko tarkasti tai pienimmän neliösumman mielessä.
Esimerkki: suoran y = a + b x sovitus datapisteisiin. Generoidaan pisteet x = 0,1,2,...10 ja y = 1 + 2x + epsilon, missä epsilon on nomaalijakautunut satunnaismuuttuja, odotusarvona 0 ja hajontana 0.5. Sovitetaan pienimmän neliösumman regressiosuora tähän pistejoukkoon.
x = linspace(0,1,10)'; y=2*x+1 + randn(10,1)*0.5; A = [ones(length(x),1) x] b=A\y xx=linspace(min(x),max(x)); plot(x,y,'o',xx,b(1)+xx*b(2))
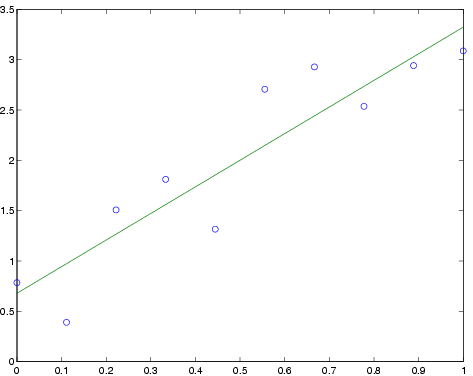
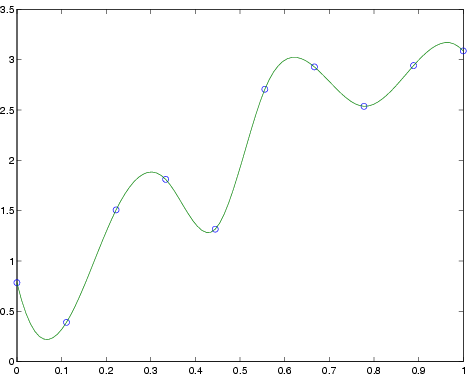
Splini-interpolaatiossa sovitetaan datapisteiden kautta kulkemaan
paloittain määritelty käyrä, joka on kahden vierekkäinen x-datapisteen
välissä kolmannen asteen polynomi ja jossa lisäksi asetetaan
ensimmäiset ja toiset derivaatat datapisteissä samoiksi. Näin
saadaan sovitus, joka usein näyttää kulkevan jouhevasti datapisteiden
kautta. Splinisovitus saadaan komennolla spline,
edellisen esimerkin datapisteisiin yksinkertaisimmillaan komennolla
» plot(x,y,'o',xx,spline(x,y,xx))
Epälineaariset yhtälöt ja yhtälöryhmät eivät ratkea
yksinkertaisilla matriisioperaatioilla vaan tarvitaan iteratiivisia
ratkaisijoita. MATLABissa reaalifunktion nollakohtaa voi etsiä
funktion fzero avulla. Polynomiyhtälöä varten on
funktio roots.
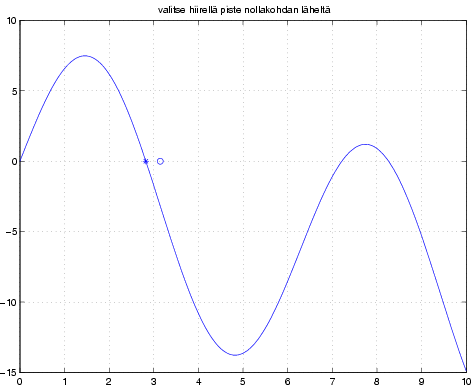
Piirretään funktio 9sin(x)-x ja valitaan hiirellä klikkaamalla alkuarvaus nollakohdalle.
» f=inline('9*sin(x)-x');
» fplot(f,[0 10]); grid
» title('valitse hiirellä piste nollakohdan läheltä')
» [x0,y] = ginput(1);
» hold on
» plot(x0,0,'o');
» x00=fzero(f,x0);
» plot(x00,f(x00),'*')
Reaaliarvoisen funktion f(x) määrätty integraali
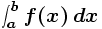
quad ja
quadl.
Sinifunktion integraali välillä [0, 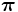 /2]
/2]
» quad('sin',0,pi/2)
ans =
1.0000
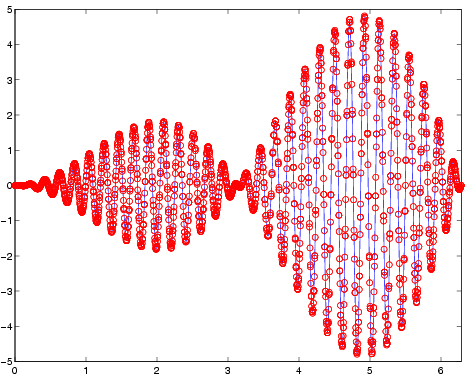
Integroidaan funktio x cos(30x) sin(x) välillä [0,2 ]. Tehdään
MATLAB-funktion sisään globaali laskuri, jotta nähdään kuinka monta
kertaan funktiota on kutsuttu. Lisäksi talletetaan evaluointipisteet
ja plotataan kuva.
]. Tehdään
MATLAB-funktion sisään globaali laskuri, jotta nähdään kuinka monta
kertaan funktiota on kutsuttu. Lisäksi talletetaan evaluointipisteet
ja plotataan kuva.
» type fun function y=fun(x) global samples count samples= [samples,x]; count=count+length(x); y=x.*cos(30*x).*sin(x);
» global count samples
» count=0; samples=[];
» I=quadl('fun',0,2*pi)
I =
0.0069891
» count
count =
1908
» fplot('fun',[0,2*pi])
» hold on; plot(samples',fun(samples),'or'); hold off
MATLABin perusasennuksessa on mukana laskentarutiinit tavallisten
1. kertaluvun differentiaaliyhtälöryhmien alkuarvotehtävien
ratkaisemiseksi. Funktiot ode45,
ode23 ja ode15s. Katso myös
help odefile. Korkeampaa kertalukua olevat
tavalliset dy:t on muutettavan 1. kl:n muotoon ennen
ratkaisua. Osittaisdifferentiaalityhtälöiden ratkaisijoita on
Differential Equation Toolbox:ssa
Esimerkki: Toisen kertaluvun tehtävä putoavasta kappaleesta, jossa ilmanvastus on suoraan verrannollinen nopeuteen ja kääntäen verrannollinen massaan
MATLAB-ratkaisua varten kirjoitetaan oma "systeemifunktio" muotoa
function ydot=omafun(t,y)
missä t on ajanhetki ja y on hetken t
tilanne. Funktio palauttaa derivaatat hetkellä t.
function ydot=pallo_putoaa(t,y) m = 0.125; g=9.81; ydot(1) = y(2); ydot(2) = -g-y(2)/m; % a(t) = vauhti ydot=ydot(:); % ydot:n oltava pystyvektori
MATLAB-ode-ratkaisijan syntaksi on
odexx('odefile',aikavektori,alkuarvot)
» aika = linspace(0,4);
» H = 10; v0=0;
» [t,y]=ode45('pallo_putoaa',aika,[H,v0]);
» plot(t,y(:,1))
MATLABin optimointirutiineita ovat fminsearch ja
fminbnd. Erillisessä Optimization
Toolbox:ssa on lisää rutiineita.