MATLAB on alunperin fortran-ohjelmointikielellä kirjoitettu matriisienkäsittelyohjelma, jonka tarkoituksena oli olla interaktiivinen ja helppo tapa käyttää LINPACK- ja EISPACK-projektien matriisialgoritmeja.
Alkuperäinen MATLAB oli julkisohjelma, jota levitettiin yliopistoille. Nykyisin käytettävissä olevat versiot ovat The MathWorks Inc.:n toimittamia kaupallisia tuotteita, joihin on tehty lukuisia parannuksia alkuperäiseen MATLAB-ohjelmaan verrattuna.
MATLABin hyviä puolia:

HUOM: Tekstissä ovat monet MATLAB-funktiot linkkejä MATLABin avustustoiminnon ohjeteksteihin ja viittaavat MathWorks'n HelpDesk-sivustoon osoitteessa http://www.mathworks.com/access/helpdesk/help/techdoc/ref/.
MATLABin kehote on ». Ulos pääsee komennolla
exit tai quit. MATLAB-komennot on ryhmitelty
tiettyihin ryhmiin; pelkkä help antaa luettelon näistä
ryhmistä ja help ryhmän_nimi listaa kaikki ryhmän
komennot ja luonnollisesti help komento antaa
lyhyen selostuksen halutusta komennosta. Aikaisempia syötteitä voi
selata ja editoida nuolinäppäinten avulla. Myös Matlab Help Desk sisältää MATLAB-komentojen
helpin
Sijoitusoperaattorina on =, siis komento
x=1 antaa muuttujalle x arvon
yksi. Puolipiste estää tulostuksen. Useampia käskyjä voi kirjoittaa
samalle riville puolipisteellä erotettuna (ei tulostusta) tai pilkulla
erotettuna (tulostus). Kokeile seuraavia:
x=2;y=3; x=2,y=3
Arvon voi poistaa komennolla clear, siis
clear x, tai jos poistetaan useampia arvoja yhdellä kertaa
clear x y. Edellä x:n ja y:n väliin pitää
laittaa välilyönti eikä esimerkiksi pilkku. Kokeile mitä antaa
x=2;y=3;clear x,y
MATLAB tuntee muun muassa vakiot pi (siis 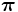 ) ja
) ja
i (imaginaariyksikkö). Jos haluat nähdä enemmän 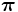 :n
desimaaleja, anna komento
:n
desimaaleja, anna komento format long. Tämän jälkeen kaikissa
tulosteissa annetaan paljon desimaaleja, kunnes komennolla format
short palautetaan alkuperäinen tilanne. Sisäiseen laskentaan tämä
ei vaikuta. Vakiot realmax ja realmin
antavat suurimman ja (itseisarvoltaan) pienimmän nollasta poikkeavan
liukuluvun, jonka MATLAB pystyy esittämään. Muuttuja eps on
liukulukulaskennassa käytettävä suhteellinen tarkkuus. Jos yrität
jakaa nollalla, tulee tulokseksi
Inf. Määrittelemätön tulos,
vaikka 0/0 on NaN (not a number).
Muuttuja ans sisältää aina edellisen komennon
tuloksen. Esimerkiksi jos suoritat pi^3 (siis
potenssiinkorotus) ja haluat sitten jälkeenpäin sijoittaa tuloksen
johonkin muuttujaan, niin se on onnistuu suorittamalla
x=ans. Kokeile. Edellistä aikaisempiin tuloksiin ei tällä
tavalla voi viitata.
MATLAB tuntee mm. seuraavat alkeisfunktiot:
abs,
sign,
sqrt,
exp,
log,
log10,
sin,
cos,
tan,
asin,
acos,
atan,
sinh,
cosh,
tanh.
Funktioita on myös helppo määritellä itse lisää. Tästä tarkemmin tuonnempana.
MATLABissa on olennaisesti vain yksi tietoalkio n×m-alkioinen numeerinen matriisi, jolla voi olla myös kompleksielementit. Erikoismerkitys voidaan tarvittaessa antaa 1×1-matriisille eli skalaarilla tai matriisille, jolla on vain yksi rivi tai sarake eli vektorille. Matriisi voidaan määritellä usealla eri tavalla:
Helpoin tapa on suoraan antaa matriisin alkiot riveittäin
käyttämällä hakasulkeita ja erottamalla rivit puolipisteellä,
';', esimerkiksi
» a=[1 2 3;4 5 6;7 8 9]
a =
1 2 3
4 5 6
7 8 9
Suurissa matriiseissa voidaan syöttö katkaista usealle riville, jolloin rivinvaihto korvaa puolipisteen.
» a=[1 2 3
4 5 6
7 8 9
]
a =
1 2 3
4 5 6
7 8 9
Matriisin eri elementit voidaan erottaa toisistaan välilyönnillä tai pilkulla. Voimme käyttää myös mitä tahansa MATLAB-laskutoimituksia elementtien laskemiseksi, esimerkiksi
» x=[-1.3,4/5,4*atan(1)] x = -1.3000 0.8000 3.1416
Käytössä on suuri joukko valmiita MATLAB-funktiota, jotka tuottavat matriiseja:
» b=hilb(5)
b =
1.0000 0.5000 0.3333 0.2500 0.2000
0.5000 0.3333 0.2500 0.2000 0.1667
0.3333 0.2500 0.2000 0.1667 0.1429
0.2500 0.2000 0.1667 0.1429 0.1250
0.2000 0.1667 0.1429 0.1250 0.1111
» c=rand(5)
c =
0.2190 0.3835 0.5297 0.4175 0.5269
0.0470 0.5194 0.6711 0.6868 0.0920
0.6789 0.8310 0.0077 0.5890 0.6539
0.6793 0.0346 0.3834 0.9304 0.4160
0.9347 0.0535 0.0668 0.8462 0.7012
Matriisien välillä toimivat suoraan perusoperaatiot +
- * / ^ ' eli
yhteenlasku, vähennyslasku, kertominen, jakolasku, potenssiin
korottaminen, sekä transpoosi. Näissä täytyy operoitavien matriisien
tietenkin olla toisilleen sopivaa tyyppiä, eli yhteenlaskussa
samanmuotoiset jne.
» a=[1 2 3;4 5 6;7 8 0], b=a'
a =
1 2 3
4 5 6
7 8 0
b =
1 4 7
2 5 8
3 6 0
» x=[-1 0 2]'
x =
-1
0
2
» c=a+b
c =
2 6 10
6 10 14
10 14 0
» y=x-1
y =
-2
-1
1
» x'*y
ans =
4
» x*y'
ans =
2 1 -1
0 0 0
-4 -2 2
» 5*a-10
ans =
-5 0 5
10 15 20
25 30 -10
Edellä näkyi esimerkki skalaarin laajennussäännöstä. Sovellettaessa laskutoimitusta skalaarin ja matriisin välillä laajennetaan skalaari samankokoiseksi matriisiksi. Edellä annetut laskutoimitukset noudattavat siis matriisilaskun sääntöjä. Jos haluamme operaation kohdistuvan suoraan matriisien elementteihin käytämme operaattorin edessä pistettä.
» a.*b
ans =
1 8 21
8 25 48
21 48 0
» a./b
ans =
1.0000 0.5000 0.4286
2.0000 1.0000 0.7500
2.3333 1.3333 NaN
Olkoon x=[3,7,1] ja y=[8,4,-2]. Näitten
vektoreitten yhteen- ja vähennyslasku onnistuu luonnollisesti
komennoilla x+y ja x-y. Entäpä kertolasku?
Vektoreillehan ei ole määritelty kertolaskua, mutta usein
MATLABia käytettäessä olisi kätevää kertoa 'vastinalkiot'
samalla tavalla kuin yhteenlaskussa lisätään vastinalkiot. Tämä
onnistuu komennolla x.*y. Huomaa, että pisteen ja
kertomerkin väliin ei saa jättää välilyöntiä. Samoin jakolasku ja
potenssiinkorotus: kokeile komentoja y./x ja
x.^2. Sama pätee matriiseille: jos A ja
B ovat samankokoisia matriiseja, niin alkioittaiset
laskutoimitukset voidaan suorittaa myös niille.
Alkioittaiset, eli "pisteittäiset" laskutoimitukset ovat +
- .* .^ ja ./. Ensin mainitut
(+, -) toimivat "luonnostaan" pisteittäin (niihin ei
siten saa lisätä pistettä). Näiden argumenttien on oltava
samankokoiset matriisit tai toisen on oltava skalaari. Tällöin
puhutaan skalaarin laajennussäännöstä: skalaari osaa
laajentua toisen argumentin kokoiseksi vakiomatriisiksi. Tämä
mahdollistaa muotoa 1+A, pi*B ym. olevat operaatiot
mielivaltaisille matriiseille A,B. (pi*B ja
pi.*B ovat samanarvoiset, koska pi on skalaari.)
Huom! Pisteen poisjääminen on aloittelevan MATLAB-urheilijan tavallisimpia virheitä.
MATLABissa on joitakin epäjohdonmukaisuuksia. Niinpä
1/v ei toimi saman periaatteen mukaan kuin yllä mainittu
pi*B, vaan 'matriisijakolasku lyö läpi' (jos v on
vektori tai matriisi), vaikka 1 onkin skalaari. Siis
pisteittäisessä jakolaskussa on aina oltava piste
(paitsi jos molemmat ovat skalaareja).
Kaikki yllä luetellut alkeisfunktiot toimivat edellisen kohdan tapaan alkioittain, joten niitten argumentti voi olla myös vektori tai matriisi. Kokeile joitakin näistä edellä määriteltyihin vektoreihin/matriiseihin.
Operaattorilla * tarkoitetaan varsinaista
matriisikertolaskua (tai sen erikoistapausta
matriisi-vektori-kertolaskua). Jakomerkkiin palataan myöhemmin.
Yksinkertainen tapa määritellä vektori perustuu
kaksoispiste-merkintään, joka on muotoa
alku:lisäys:loppu. Jos
lisäys puuttuu on se oletusarvoisesti 1.
» 0:.1:1
ans =
Columns 1 through 7
0 0.1000 0.2000 0.3000 0.4000 0.5000 0.6000
Columns 8 through 11
0.7000 0.8000 0.9000 1.0000
Jos halutaan n kappaletta arvoja tietylle välille, sen voi tehdä esimerkiksi näin:
» n=5; x=0:1/(n-1):1
x =
0 0.2500 0.5000 0.7500 1.0000
Saman asian tekee funktio linspace.
» linspace(0,1,5)
ans =
0 0.2500 0.5000 0.7500 1.0000
Matriisin yksittäisiin alkioihin voidaan viitata antamalla suluissa alkion indeksit. Antamalla indeksin paikalla vektorin voidaan valita osamatriiseja.
» a=[1 2 3;4 5 6;7 8 9];
» a(2,2)
ans =
5
» a(3,3)=a(1,3)+a(3,4)
??? Index exceeds matrix dimensions.
» a(3,3)=a(1,3)+a(3,1)
a =
1 2 3
4 5 6
7 8 10
» a(:,2)
ans =
2
5
8
» a(3,:) = [5 5 5]
a =
1 2 3
4 5 6
5 5 5
Loogisten operaattoreiden avulla voidaan myös kätevästi valita tietyt ehdot toteuttava osa matriisista.
» a<5
ans =
1 1 1
1 0 0
0 0 0
» a.*(a<5)
ans =
1 2 3
4 0 0
0 0 0
» x=fix(rand(100,1)*100); % Generoidaan satunnaisvektori
» length(x(x>90)) % Kuinka monta alkiota > 90
ans =
9
» ind=find(x>90); % Etsitään näiden indeksit
» ind(1) % Ensimmäinen niistä
ans =
17
» x(17)
ans =
98
Suuri joukko valmiita matriisifunktioita on
käytettävissä. Esimerkiksi matriisin determinantti lasketaan funktion
det avulla:
» det(a)
ans =
27
käänteismatriisi,
inv
» inv(a)
ans =
-1.7778 0.8889 -0.1111
1.5556 -0.7778 0.2222
-0.1111 0.2222 -0.1111
matriisin aste, ominaisarvot jne.
» rank(a)
ans =
3
» eig(a)
ans =
-0.3884
12.1229
-5.7345
Matriisin jakolaskuja on kaksi kappaletta, oikealta jako ja
vasemmalta jako. A/B tarkoittaa matriisia
AB-1 ja A\B matriisia
A-1B.
Vasemmalta jako \ laajenee myös
tapauksiin, jolloin käänteismatriisia A-1 ei ole
olemassa. Tällöin A\b on lineaarisen yhtälöryhmän
Ax=b pienimmän neliösumman ratkaisu. Katso
help \.
» a/b
ans =
-0.3333 0.6667 0.0000
-3.3333 3.6667 0.0000
-5.3333 4.6667 1.0000
» a\b
ans =
-0.3333 -3.3333 -5.3333
0.6667 3.6667 4.6667
0.0000 0.0000 1.0000
» (b'\a')'
ans =
-0.3333 0.6667 0.0000
-3.3333 3.6667 0.0000
-5.3333 4.6667 1.0000
» a\a
ans =
1.0000 0 0
0 1.0000 0
0 0.0000 1.0000
» inv(a)*a
ans =
1.0000 0.0000 0
0 1.0000 0
0 0.0000 1.0000
» (inv(a)*a==a\a)
ans =
1 0 1
1 1 1
1 0 1